Tabaka, klivaj, fay, damar ve çatlak gibi düzlemsel yapı
unsurları ile kıvrım eksenleri, fay ve çatlak izleri, lineasyon gibi çizgisel
yapı unsurlarının doğadaki duruşları onların doğrultu, eğim yönü ve eğim
açıları ile veya sadece eğim yönü ve eğim açıları ile gösterilir.
Doğrultu
ve doğrultu yönleri
Düzlemsel bir yapı unsurunun doğrultusu, o unsurun
kendisi ile yatay düzlemle yapmış olduğu arakesittir.
Doğrultunun değeri, arakesitin o noktadaki kuzey-güney
coğrafik doğrultuyla yapmış olduğu açının derecesidir.
Genellikle kuzeyden itibaren doğuya veya batıya doğru
olan dar açı K30D (N30E) veya K30B (N30W)
şeklinde söylenir ve yazılır.
Doğrultu iki yönlüdür, aralarında 180° lik bir açı vardır
(K30B = G30D). Bu nedenle yönlerden birinin Seçilmesiyle doğrultunun duruşu
saptanmış olur.
Çizgisel bir yapı unsurunun doğrultusu bu unsurdan geçen
düşey düzlem ile yatay düzlemin arakesitidir.
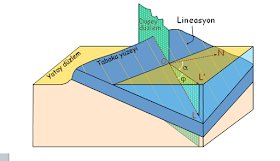
Düzlemsel yapılarda doğrultu ve eğimin, tabaka yüzeyi
örneğinde şematik olarak gösterilişi.
Düzlemsel
yapı unsurlarından olan tabaka doğrultusu, eğim yönü ve eğim açısı kavramları.
Eğim
yönü ve eğim açısı
Çizgisel bir yapı üzerinde alınan ve oku başlangıç
noktasına göre daha aşağı seviyede bulunan vektöre eğim vektörü (OE) denir.
Eğim vektörünün yatay bir düzlem üzerindeki dik
izdüşümüne ise eğim yönü vektörü (OE’)
veya eğim yönü denir.
Eğim yönü çizgisel bir yapı unsurunun doğrultusu
üzerindedir. Fakat bu doğrultunun
yönlerinden yalnızca biriyle çakışır.
Eğim vektörü
(OE) ile eğim yönü vektörü (0E’)
arasındaki açıya eğim açısı (j)
veya eğim adı verilir.
Düzlemsel bir yapının eğim vektörü (OE) düzlemin doğrultusu ile bunun
doğrultusuna dik düşey bir düzlemin arakesiti
üzerinde bulunan ve oku aşağı seviyeyi gösteren vektördür.
Eğim yönü (OE')
eğim vektörünün yatay düzlemdeki izdüşümüdür.
Eğim açısı (f); eğim vektörü (OE) ile eğim yönü
vektörü (OE') arasındaki dar açıdır. Yani, yatay düzlemle
eğik düzlem arasındaki dar açıdır.
Eğim yönü açısı (a); eğim yönü vektörünün (OE’) kuzey
ile yapmış olduğu, saat yelkovanı
yönündeki, açıdır.
Bir düzlemin eğim
yönü vektörü düzlemin doğrultusuna diktir.
Düzlemsel yapı öğelerinin duruşlarıyla ilgili terimlerin
tanıtılması. YY’= doğrultu, OE= eğim vektörü, OE’= eğim yönü vektörü, j= eğim
açısı, a= eğim açısı, YF= görünür eğim vektörü, j’=Görünür eğim açısı, x=
doğrultu ile kesit izi arasındaki açı.
Çizgisel
yapı unsurlarının öğeleri: Örnek olarak dilinim düzlemleriyle tabaka yüzeyleri
arasındaki arakesitlerin oluşturduğu lineasyonlar alınmıştır. OL= Eğim vektörü,
OL’= Eğim yönü vektörü, j= eğim açısı, a= eğim yönü açısı
Jeolog
pusulası ve çeşitli kullanımı
Brunton pusulası ve ana unsurları
Jeolog pusulası esasta pusula, klinometre (eğim ölçer) ve
el düzecinden oluşur.
Jeolojik çalışmalarda çok değişik amaçlarla kullanılırsa
da yaygın olarak düzlemsel ve çizgisel yapı unsurlarının duruşlarının (eğim
yönü ve eğim açıları) saptanmasında kullanılır.
Yerküresinin manyetik özelliğine dayanılarak yapılmış bir
jeolog pusulasının ana unsurları şunlardır:
- Pusula iğnesi (ağırlıklı taraf güneyi gösterir)
- İğne ayağı
- Pusula tabanı
- ölçek çemberi
- Nişan delikleri ve nişan kılı
- Kabarcıklı düzeçler
- Klinometre (eğim ölçer)
- Pusula tabanı üzerinde yön harfleri (N: kuzey, S: güney, E: doğu, W: Batı). Taban üzerinde E-W yer değiştirmiş olarak yazılıdır. Çünkü pusula tabanını saat ibresi yönünde döndürdüğümüzde pusula iğnesi saat ibresinin tersi yönünde dönme hareketi yapar.
Brunton cep pusulasının kapalı görünümü.
Brunton cep pusulasının açık görünümü
Pusula
okuma kuralı
Pusula tabanının N-S çizgisi, ölçülecek yön doğrultusuna,
ya pusulayı bitiştirerek ya da nişan alma yoluyla paralel duruma getirilir,
Pusula tabanı,
kabarcıklı düzeçten yararlanılarak yatayla konuma getirilir,
Bu iki işlem yapıldıktan sonra, iğne bağlama vidası
serbest bırakılır,
İğnenin salınımı durduktan sonra yön açısı okunur.
Yön açısı okunurken pusula okuma kuralı dikkate alınır.
Şöyle ki:
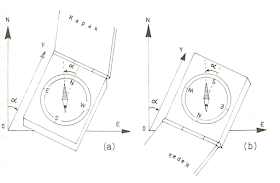
- Bir OY yönü ölçülürken eğer pusula tabanının N harfi yön tarafında ise değer iğnenin kuzey; S harfi yön tarafında ise değer iğnenin güney ucundan okunur.
Pusula okuma kuralının
gösterilişi
Pusulanın bir bölgedeki grid
kuzeyine bağlanması
Basılı topoğrafik haritalar genel olarak grid enlem ve
boylamları ile taranmıştır.
Pusula ile ölçülen yönler haritadaki grid yönlerine
uymaz;
Grid kuzeyi ile manyetik kuzey arasında değeri zamana
bağlı olarak değişen ve iğne sapması olarak isimlendirilen bir açı
bulunmaktadır.
Bazı bölgelerde manyetik kuzey grid kuzeyinin batısında,
diğer bazı bölgelerde ise doğu tarafındadır. Bu durumlar basılı haritalarda
gösterilmektedir.
Grid koordinatları taşıyan bir topoğrafik harita üzerinde
iki belirgin nokta seçelim ve bunları A ve B olarak adlandıralım. Bu iki
noktadan bir fayın geçtiğini düşünelim.
Bu fayın doğrultu yönlerinden biri, örneğin AB yönü,
pusula kullanılmadan, harita üzerinde grid kuzeyi referans alınarak açı ölçerle
ölçelim. Bu değere a1 diyelim.
Sonra arazide A noktasında durup, pusulayla AB yönünü
ölçelim. Bulduğumuz değer de a2 olsun. Bu iki değer bir biriyle
karşılaştırıldığında farklı oldukları görülür.
Her iki değer arasında a2 =a1+|x | şeklinde bir bağıntı bulunmaktadır.
Burada x bölgeye ait iğne sapması demektir.
Eğer bölgede manyetik kuzey grid kuzeyinin batısında ise,
eşitlikte x’in değeri (+); doğusunda ise (-) olur.
Grid enlem ve boylamı ile taranmış bir haritada her hangi
bir AB yönünün ölçülmesi. a1 grid kuzeyine; a2 ise
manyetik kuzeye göre ölçülen değerlerdir. Aralarındaki fark iğne sapması (x) olarak
adlandırılır.
Manyetik kuzey ile grid kuzeyi arasındaki bölgesel iğne
sapmalarının durumu.
a-)
Manyetik kuzey grid kuzeyinin doğusundadır; bu durumda
x=
a1-a2,
b-)
Manyetik kuzey grid kuzeyinin batısındadır; bu durumda ise,
x= a2-a1
Bir bölgede yapılan yön ölçümlerinin
yukarıdaki eşitlik yardımıyla teker teker grid yönüne göre değiştirilmesi yerine, ölçümleri yapmadan önce,
pusula ayar vidasıyla,
ölçek çemberi x açısının değeri kadar çevrilir.Bunun için pusula ayar kuralı dikkate
almak gerekir. Şöyle ki:
- Bir bölgede grid kuzeyi manyetik kuzeyin x°batısında ise, ölçek çemberi x° batıdan doğuya;
- Grid kuzeyi manyetik kuzeyin doğusunda ise, ölçek çemberi x° doğudan batıya çevrilerek pusula bölge grid yönlerine bağlanmış olur.
Pusula ile yapılan ölçmeler
Jeolog pusulasının kullanım alanları şunlardır:
- Düzlemsel ve çizgisel yapı unsurlarının (tabaka, fay, foliasyon, kıvrım ekseni, lineasyon vb.) doğrultu, eğim yönü ve eğim açılarının ölçülmesi,
- Travers (poligon) çizimleri,
- İki nokta arasındaki yükseklik farkının ölçülmesi
- Yamaç eğiminin Ölçülmesi
- Kestirme yöntemiyle harita üzerinde yer tayini
- Eş yükseklik eğrilerinin çizimi
Pusula
ile yön ölçümü (yatay açı ölçümü)
- Pusula ile herhangi bir AB yönü ölçülmek istendiğinde şu işlemler göz önünde bulundurulmalıdır.
- Pusula yatay tutulmalıdır,
- Nişan noktası, nişan delikleri ve nişan kılı üzerinde olmalıdır,
- İğne durmalıdır,
- Okuma pusula okuma kuralına göre yapılmalıdır.
Eğer nişan alınan nokta bel hizasında (+1m de) ise;
- Pusula kapağı 135° kadar açılır, nişan kolu yatırılarak ucu kırılır.
- Jeolog ayaklarını az açarak pusulayı sol avuç içinde bel hizasında tutar.
- Pusula yataylanır (yuvarlak düzecin kabarcığı ortaya getirilir).
- Nişan alınan nokta ile nişan kolu ucu aynada gözükecek şekilde ayna sağ elle ayarlanır.
- Pusula yatay olarak düşey eksen etrafında döndürülür.Böylece nişan alman noktanın aynadaki görüntüsü ilenişan kolu ucu aynadaki nişan kılı üzerine getirilir.
- İğne salınımı durunca pusula okuma kuralına göre okuma yapılır.
Jeolog pusulası ile bel hizasında
nişan alma
(yatay açının ölçülmesi).
Nişan alınan nokta göz düzeyinde
ise,
- Nişan kolu yatırılarak kapak 45° açılır.
- Pusula sol elle göz düzeyinde, nişan kolu yanında gözden 30 cm kadar uzakta tutulur.
- Aynadan yuvarlak düzece bakılarak pusula tabanın yataylanması sağlanır. Daha sonra gözlenen nokta, kapaktaki nişan gözü kılı ve katlanır büyük nişan kolu aynı doğrultuya gelecek şekilde pusula döndürülür.
- Yatay konumu bozmadan aynadan yön değeri yine pusula okuma kuralına göre okunur.
- Alıştırmalarla l°-2° yi . geçmeyen ölçmeler yapılmalıdır .
Pusula ile düşey açıların ölçümü
Düşey açının okunabilmesi için pusulanın klinometresi şu
şekilde kullanılır.
- Pusula kapağı 45° açılarak nişan kolu uzatılır ve ucu 90° kırılır.
- Pusula düşey düzlemde yan tutularak nişan kolu sağ göz yanında olmak üzere tutulur.
- Gözlenen nokta, kapaktaki nişan gözü ve kılı, nişan kolundaki nişan gözü, üçü bir doğrultuya getirilinceye kadar pusula eğilir.
- Pusula kutusu arkasındaki kol ile klinometrenin kabarcıklı düzeci aynadan bakılarak ortalanır.
- Nişan öğelerinin hizası kontrol edildikten sonra pusula indirilerek açı içteki çemberden okunur.
Brunton pusulası ile düşey açıların ölçülmesi
Pusula ile iki nokta arasındaki
yükseklik farkının bulunması
Durulan nokta ile nişan alınan nokta arasındaki yükseklik
farkı için,
- Yamaç uzaklığı (QS) adımlama ile bulunur. Düşey açı (M) pusula ile ölçülür ve,yükseklik farkı (SP) =yamaç uzaklığı (QS)x sin M formülünden veya;
İki nokta arasındaki yatay uzaklık (QP) haritadan
bulunarak SP=QP.tan M formülünde yerine konursa yükseklik farkı bulunmuş olur.
Burada yamaç eğim açısını bulurken dikkat edilecek nokta
pusulanın nişan alınan noktadan göz hizası kadar daha yüksek bir yere nişan
alınmasıdır.
Brunton pusulası ile iki nokta arasındaki yükseklik
farkının bulunması,
a) Göz
yüksekliğindeki bir noktadan nişan alındığı zamanki durum,
b) Noktaya yamaç
aşağı bir noktadan nişan alındığı zamanki durum.
M: Düşey açı, sp:
Yükseklik farkı, QS: Yamaç uzaklığı, QP: Yatay yamaç uzaklığı
İki nokta arasındaki yükseklik farkı pusula nivo aleti
gibi kullanılarak da bulunabilir. Bunun için:
- Klinometre O'a getirilir. Pusula kapağı 45° açılarak nişan kolu uzatılır ve ucu da yukarı bükülür,
- Pusula göz hizasında tutularak silindirik düzeç aynadan bakılarak ortalanır.
- Pusulanın nişan kolundaki nişan deliği ile kapaktaki nişan gözündeki kılı birleştiren doğrunun araziyi kestiği nokta akılda tutulur.
- Akılda tutulan noktaya gidilerek yukarıdaki işlemler tekrarlanır,
- Yapılan ölçüm sayısı ile jeologun göz hizasına kadar olan boyu çarpılırsa iki nokta arasındaki yükseklik farkı bulunmuş olur .
Pusula yardımıyla eş yükseklik eğrilerinin çizimi.
Pusula ile düzlemsel ve çizgisel
yapı unsurlarının eğim yönü ve eğim açılarının ölçülmesi
Eğim açısının büyüklüğüne göre bir yapısal unsur f = 0° (yatay), 0 < f < 90°
(eğik) veya f = 90° (dik) durumlarında bulunabilir.
Düzlemsel yapı unsurlarında eğim
yönü ve eğim açısının ölçülmesi
Bu iş için pusula kapağı ölçülecek düzleme bitiştirilir.
Eğer düzlemin
üzeri düzgün değilse jeolog defterinden yararlanılabilir.
Pusula tabanı düzeç yardımıyla yataylanır ve pusula okuma
kuralına göre değer doğrudan okunur.
Buna göre,
- Eğik düzlemlerde (0° < f < 90°), mostra durumuna göre, düzleminin alt veya üst yüzeyinden ölçü alınması gerekebilir. Ancak her iki halde de ölçülen ve okunan OE' eğim yönü vektörüdür. Önemli olan pusula okuma kuralına uymaktır.
- Şayet pusula kapağı düzleme dayandırıldığında pusula tabanın N yi tabakanın eğim yönü tarafında ise okuma iğnenin kuzey ucundan yapılır. Aksi halde güney ucundan okunur.
Düzlemsel yapılarda pusulayla eğim yönünün ölçülmesi.
a-Eğik,
b- Düşey,
c- Yatay duruşlu düzlemler.
OE- Eğim vektörü, OE’- Eğim yönü vektörü, j- Eğim açısı.
Eğim yönü bulunduktan sonra düzlemin eğim açısını ölçmek
için:
- Pusula tabanı düşey duruma getirilip eğim vektörü üzerine yerleştirilir.
- Sonra pusula kutusu arkasındaki kol yardımıyla klinometrenin düzeci ortalanır ve eğim açısı okunur.
- Eğer pusula tam olarak eğim vektörü üzerine konmaz ise ölçülen eğim açısı görünür eğim açısı (j) olur.
Düzlemsel
yapı unsurlarının eğim vektörü (OE) üzerinde pusula ile eğim açısının (j)
ölçülmesi.